Deep reinforcement learning(1): Policy gradient

此系列主要为 UCB CS285 深度强化学习系列课程学习笔记。

1. 问题描述

1.1 概率模型

忽略观测误差，深度强化学习解决的问题可以写成如下形式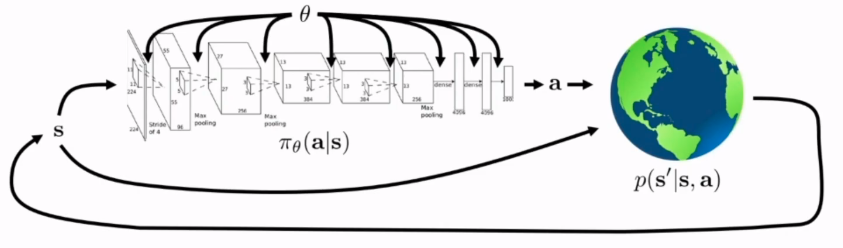： 整个概率模型主要由两个部分组成，首先由当前状态\(s\)通过当前的策略\(\pi_\theta\)得到动作的概率分布，在动作的状态分布中采样得到下一步真正需要采取的动作\(a\)，将\(a\)作用于实际系统中得到下一个状态的概率分布\(p(s'|s,a)\)，实际系统生成反馈状态并形成闭环。

假设我们想研究未来\(T\)时刻内策略参数设定为\(\theta\)的模型，这整个概率分布模型可以写成：

\[ p_\theta(s_1,a_1,s_2,a_2\dots s_T,a_T)=p(s_1)\prod_{i=1}^T\pi_\theta(a_i|s_i)p(s_{i+1}|s_i,a_i) \]

之后的表述会将整条状态轨迹写成\(\tau\)，即 \(p_\theta(\tau)=p_\theta(s_1,a_1,s_2,a_2\dots s_T,a_T)\)

1.2 目标函数

在得到上述概率模型后，我们需要明确需要优化的是什么。一般优化目标是关于动作和状态的函数，仍然假设我们要研究未来\(T\)时刻内的策略，目标函数可以被写成：

\[ J(\theta)=\mathbb E_{\tau\sim p_\theta(\tau)}\left[\sum_{i=1}^Tr(s_i,a_i)\right] \]

深度强化学习的目标即通过调整\(\theta\)使得目标函数的期望最大化。

2. 策略梯度

2.1 REINFORCE法

在得到上述的问题描述后，最简单直接的方法就是直接求目标函数对\(\theta\)的梯度，之后用梯度上升法（因为需要最大化目标函数）逐步优化参数。这就是策略梯度的基本思想。

\[\nabla_\theta J(\theta)=\int\nabla_\theta p_\theta(\tau)r(\tau)d\tau\]

上面这个式子中，\(r(\tau)\) 表示对特定轨迹 \(\tau\) 的累计误差，积分的含义则表示在给定指定参数 \(\theta\) 的情况下，由于对应每个状态的动作并不是确定的，所以最后生成的轨迹会存在多种可能性，积分就是对这些轨迹的概率分布积分。下一步为了求解这一项，我们会引入一个 \(\log\) 函数的trick：

\[ p_\theta(\tau)\nabla_\theta\log p_\theta(\tau)=p_\theta(\tau) \frac{\nabla_\theta p_\theta(\tau)}{p_\theta(\tau)}=\nabla_\theta p_\theta(\tau) \]

根据这个trick我们对之前的积分进行变换：

\[ \begin{align*} \nabla_\theta J(\theta)&=\int\nabla_\theta p_\theta(\tau)r(\tau)d\tau\\ &=\int p_\theta(\tau)\nabla_\theta\log p_\theta(\tau) r(\tau)d\tau\\ &=\mathbb{E}\left[\nabla_\theta\log p_\theta(\tau) r(\tau)\right] \end{align*} \]

把之前的概率分布代入这个式子中，由于是对 \(\theta\) 求梯度，初始状态概率分布以及状态转移分布都可以被忽略（与 \(\theta\) 无关），最后梯度可以被写成：

\[ \nabla_\theta J(\theta)=\mathbb{E}_{\tau\sim p_\theta(\tau)}\left[\left(\sum_{i=1}^T\nabla_\theta\log\pi_\theta(a_i|s_i)\right) r(\tau)\right] \]

写成这个形式后我们就能通过采样的方法计算梯度，并采用梯度上升法来优化参数 \(\theta\)。这就是最基本的策略梯度REINFORCE方法：

1. 从 \(\pi_\theta(a|s)\) 中采样得到一系列轨迹 \(\tau_i\)
2. 通过上述计算对当前策略进行评价，算出 \(J_\theta(\theta)\) 和梯度
3. 对参数进行梯度下降

为了更深入理解这个梯度计算的形式，我们可以将它和监督学习的情况做对比。假设对于同样一个任务，我们还是需要学习特定状态下应该采取的行动 \(\pi_\theta(a|s)\)， 不同的是这次我们有一系列已经标记过的数据 \((s_i,a_i)\)，我们假设这些数据对应的策略就是最优策略，而我们就是要学习这个策略，这个问题就被变成一个监督学习问题。而此时目标函数的梯度可以写成如下形式：

\[ \nabla_{\theta} J_{\mathrm{ML}}(\theta) \approx \frac{1}{N} \sum_{i=1}^{N}\left(\sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right)\right) \]

这里本质上就是最大似然估计，即通过训练使得标记的策略出现的可能性最大。不难发现这与我们推导出的梯度只相差一项 \(r(\tau)\) 即整条轨迹上累计的回报。这里的直观理解就是最大似然估计会让给定的轨迹出现概率最大，而策略梯度法会让带有最大回报的轨迹出现概率最大。

2.2 减小方差

如果我们直接使用上述方法对系统进行控制，通常会有很大的问题。其中一个问题就是梯度的方差过大，假设我们在每一步 \(r(a_i,s_i)\) 上都加一个相同的常数，理论上这个系统和之前的没有区别，但是计算梯度时会产生很大的差别。

2.2.1 通过因果关系简化梯度计算

为了减少上面提到的方差问题，我们首先想到的是减小 \(\nabla_\theta J(\theta)\) 的值。这里可以通过因果关系得到小结论：假设我们有 \(t<t'\) ，那么 \(t'\) 时刻的策略不会影响 \(t\) 时刻的回报。根据这个结论，我们可以在计算梯度时 只将 \(t\) 时刻后的回报和 \(t\) 时刻的似然概率相乘，并且能够证明这样得到的结果仍然是梯度的无偏估计：

\[ \begin{align*} \nabla_{\theta} J(\theta) &\approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right)\left(\sum_{t^{\prime}=1}^{T} r\left(\mathbf{s}_{i, t^{\prime}}, \mathbf{a}_{i, t^{\prime}}\right)\right)\\ &= \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right)\left(\sum_{t^{\prime}=t}^{T} r\left(\mathbf{s}_{i, t^{\prime}}, \mathbf{a}_{i, t^{\prime}}\right)\right) \end{align*} \]

2.2.2 通过baseline方法减小方差

这里的指导思想是，当我们评价一条轨迹的好坏时，我们先得到一个回报的平均值，再比较新的轨迹的回报与这个平均值。数学表达如下：

\[ \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i, t} \mid \mathbf{s}_{i, t}\right)\left(\mathbb{r}(\tau)-b\right) \]

\[ b = \frac{1}{N}\sum_{i=1}^N r(\tau) \]

我们可以证明通过这种方法，策略梯度的期望不会被改变，而方差则会减少。