Deep reinforcement learning(2): Actor-Critic

1. 从策略梯度到Actor-Critic

上一章介绍了策略梯度的基本思想，最后得到的更新梯度的步骤可以写成如下形式： $${\mathrm{\nabla }}_{\theta }J(\theta )\approx \frac{1}{N}\sum _{i=1}^N\sum _{t=1}^T{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }({\mathbf{a}}_{i,t}\mid {\mathbf{s}}_{i,t})(\mathbb{r}(\tau )-b)$$ 这里的问题是 $r(\tau )$ 这一项是通过蒙特卡罗方法从 ${\pi }_{\theta }(a|s)$ 中采样得到的，如果我们希望agent在与环境交互一次后就进行一次参数的优化，这里得到的梯度则只能根据单个样本计算，即得到一条轨迹后就代入上面的式子计算梯度，这样得到的结果很显然会有很大的方差。

为了解决这个问题，在Actor-Critic算法中，我们用Q函数来代替 $r(\tau )$，并且创建Critic网络来拟合Q函数。这样我们将梯度重新写成： $${\mathrm{\nabla }}_{\theta }J(\theta )=\frac{1}{N}\sum _{i=1}^N\sum _{t=1}^T{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }({\mathbf{a}}_{i,t}\mid {\mathbf{s}}_{i,t})(Q_{\theta }({\mathbf{a}}_{i,t},{\mathbf{s}}_{i,t}))$$ Critic函数最后训练的目标是让 $Q_{\theta }(\mathbf{a},\mathbf{s})$ 接近 ${\mathbb{E}}_{\theta }[r(\tau )]$，直观上理解就是我们通过已经收集到的reward拟合出一个函数来评估当前状态的好坏。和之前直接用每条轨迹的reward相比，这种方法保留了历史reward的信息，因此更加可靠。

这里我们还没有讨论具体该如何训练Critic网络。事实上在之后的推导中我们将会用监督学习来训练Critic网络，具体如何实现以及监督学习的训练集如何生成会在下一节里提到。

2. 从AC到A2C

基本的AC算法中我们在Critic网络中需要以state和action作为输入，输出Q函数。这样会带来两个问题：1.方差仍然很大；2.输入维度大（包括状态输入 $s$ 和动作输入 $a$），训练困难。为了解决这些问题我们对AC算法进行一些改进。

2.1 引入基线

首先和Policy gradient里一样，我们同样可以通过引入基线的办法来减小方差。这里的基线可以直接定义为给定状态情况下的价值函数 $V_{\theta }(s)$。与 $Q_{\theta }(a,s)$ 相比，价值函数还没有对当前状态做出动作的选择，因此可以被当做是平均之后的 $Q(a,s)$ 函数。引入价值函数作为基线后，梯度可以重新被写成：

$${\mathrm{\nabla }}_{\theta }J(\theta )=\frac{1}{N}\sum _{i=1}^N\sum _{t=1}^T{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }({\mathbf{a}}_{i,t}\mid {\mathbf{s}}_{i,t})(A_{\theta }({\mathbf{a}}_{i,t},{\mathbf{s}}_{i,t}))$$

其中 $A_{\theta }(a_t,s_t)$ 函数我们定义为优势函数： $$\begin{array}{rl}{A}_{\theta }(a_t,s_t)& =Q_{\theta }(a_t,s_t)-V_{\theta }(s_t)\end{array}$$

事实上，这里的基线我们只需要选择一个与当前动作无关的函数，我们就能证明这里的梯度仍然是无偏估计。证明之后有空补上！

2.2 自助法采样(Bootstrapping)

这里改进的基本思想是：如果我们需要采样一条轨迹来拟合优势函数，那采样的方差会特别大。然而如果我们只采样下一步的状态，方差相比采样整条轨迹就会大幅减小。

$$$$

在这样近似之后，由于reward函数已知，我们只需要对价值函数进行拟合就能推算出优势函数。这样输入维度就只有状态变量了，大大节省了训练难度。

2.3 生成训练集

到此为止我们确定了我们需要拟合的函数就是价值函数 $$$$，前文中提到，我们将会用监督学习的方法来拟合价值函数。即定义损失函数：$$$$ ，同时收集训练集：$$$$ 来优化损失函数。如何生成训练集就是我们接下来要讨论的问题。

2.3.1 蒙特卡罗方法生成训练集

最直观的方法就是我们直接通过采样一整条轨迹作为训练集。这里假设我们是通过与实际环境进行交互得到的轨迹，在这种情况下我们通常无法“重置”一个状态，这就意味着我们将会只有单样本的训练集（对于一个状态 $$$$ 我们只能生成一次轨迹来预测状态 $$$$ 之后 $$$$ 步的回报,理想情况下由于策略具有不确定性，我们是希望能够多次从一个状态出发，得到之后 $$$$ 步的回报之后取平均值来减小预测的方差）。

利用蒙特卡罗方法得到的训练集可以写成：$$$$

2.3.2 自助法估计训练集

和之前一样，我们可以用自助法估计 $$$$ 时刻的状态，从而将累计回报近似为 $$$$ 的形式。（与之前不同的是这里我们是对 $$$$ 进行估计，在只有 $$$$ 的情况下我们事实上需要多估计一步 $$$$，我认为这里事实上进行了两步Bootstrapping）。

$$$$

这里的问题是即使我们拓展成这种形式，最根本的问题还是没有解决，我们不知道 $$$$ 的值。这里的解决办法就是假设上一次迭代得到的 $$$$ 与这次的差距很小，我们直接拿上一次的价值函数作为这次的估计。很显然这是个 有偏估计，需要我们用其他实际的工程技巧来克服这个问题。

目前为止我们讨论的都是有限时间序列的情况，并且我们认为时间 $$$$ 是被计算到状态变量中的。假设我们现在需要解决无限时间序列，并且不考虑把时间 $$$$ 作为状态考虑。这种情况下由于我们不断在价值函数上加一步回报 $$$$，如果单步回报的期望大于0，那拟合的价值函数就会随迭代次数增加而不断增加，无法收敛。为了解决这个问题我们引入类似贝尔曼方程里的折扣因子的概念： $$$$ 至此我们就得到了完成的A2C算法流程。

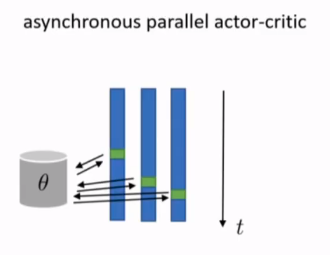
3. 从A2C到A3C

原理很简单：同时让多个actor与环境分别单独进行交互，将交互的结果存入缓冲区中总结reward后统一对参数进行更新。